Ip address

Pengertian IP Address Beserta Fungsi dan Kelas IP Address pada Jaringan Komputer

 Hermawan  Jaringan, Komputer, Networking 10/02/2019

Bagi mereka yang sedang berkonsentrasi pada bidang jaringan komputer atau dunia internet pasti akan sering mendengar dan berinteraksi dengan yang namanya IP Address. Jaringan komputer adalah suatu bentuk jaringan telekomunikasi yang saling dihubungkan pada beberapa komputer dengan tujuan agar bisa saling berinteraksi dan saling tukar – menukar data.

Pada umumnya semua jaringan komputer didesain dengan model client-server. Terdapat komputer yang bertugas sebagai server dan beberapa komputer yang bertindak sebagai client atau anggota. Penggunaan IP Address dalam hal ini adalah sebagai identitas dari masing – masing komputer baik yang bertindak sebagai server maupun sebagai client. Sama halnya dalam aktivitas internet, penggunaan IP Address juga sebagai penamaan atau identitas dari masing – masing komputer host.

Pada dasar nya IP Address berbentuk kombinasi angka dalam digit tertentu dan dipisah oleh titik. Untuk dapat menentukan pemakaian IP Address pada masing – masing komputer tentunya juga memerlukan dasar – dasar ilmu dan pemahaman yang mendalam.

Meskipun membaca pedoman tapi tanpa adanya pemahaman tentu setiap orang akan kesulitan untuk mengimplementasikan IP Address. Oleh karena itu kami akan mendeskripsikan dan menjelaskan secara detail pengertian IP Address dan fungsinya kepada anda. Selain itu anda juga akan mengetahui kelas – kelas yang ada dalam IP Address.

Daftar Isi

Pengertian IP Address

Pada dasarnya Internet Protocol Address atau biasa disebut IP Address merupakan suatu deretan angka biner yang disusun dengan kisaran antara 32 bit sampai dengan 128 bit dan digunakan sebagai alamat identifikasi pada masing – masing komputer. Dalam ilmu jaringan komputer penggunaan angka dengan 32 bit dipakai pada IP Address khusus versi IPv4 sedangkan untuk angka 128 bit untuk yang versi IPv6.

Hadirnya versi IPv6 untuk mengantisipasi jika IPv4 sudah kehabisan daya tampung mengingat kemajuan teknologi yang tentunya mendorong juga semakin berkurangnya persediaan IP Address untuk seluruh dunia. Semakin tinggi bit pada IP Address komputer anda tentunya akan menghadirkan koneksi yang lebih cepat tentunya.

Selain IP Address, dalam jaringan komputer juga dikenal istilah DNS Server dan DHCP Server. Ketiga istilah berperan penting untuk menunjang pemakaian komputer anda dalam suatu sistem jaringan. Biasanya pada DHCP Server client akan menerima pengalamatan IP Address yang sudah disetting secara otomatis. Sedangkan untuk DNS Server, penggunaan IP Address untuk mensetting hanya pada Ipv4.

Fungsi IP Address

Setelah memahami definisi dan cara kerja IP Address maka anda juga harus mengetahui fungsi utamanya. Terdapat 2 fungsi khusus mengapa harus menggunakan IP Address pada sistem komputer jaringan yakni sebagai alat identifikasi host dan sebagai alamat lokasi jaringan pada setiap komputer. Secara detail akan dijelaskan dibawah ini :

1. IP Address sebagai alat identifikasi host

Seperti yang sudah kami jelaskan sebelumnya, jika komputer diibaratkan sebagai manusia maka IP Address akan digunakan sebagai nama atau identitas terutama dalam semua aktifitas yang berhubungan dengan jaringan. Pada sistem jaringan komputer dikenal istilah host dan penggunaan IP Address dimaksudkan untuk mengidentifikasi masing – masing host. Tentu saja tidak boleh ada host yang memiliki IP Address sama.

2. IP Address sebagai alamat lokasi jaringan

Selain sebagai identifikasi host penggunaan IP Address juga dimaksudkan sebagai alamat lokasi jaringan. Maksudnya adalah penamaan IP Address bisa memberikan informasi dari negara mana komputer atau host yang dimaksud. Fungsi ini biasanya dijalankan pada aktivitas menggunakan internet karena dengan IP Address data bisa sampai pada komputer yang tepat. Untuk memeriksa IP Address bisa melalui setting jaringan atau menggunakan web browser.

Kelas pada IP address

Seperti yang sudah dijelaskan bahwa IP Address terdiri atas dua versi yakni IPv4 dan IPv6. Namun wajib anda ketahui bahwa di versi IPv4 saja tersedia setidaknya daya tampung sebanyak kurang lebih 4.294.967.296 host di seluruh dunia. Dengan jumlah yang sangat banyak seperti itu maka tentunya akan menyulitkan dari segi pemilihan dan penggunaannya. Oleh karena itu diperlukan adanya penggolongan IP Address menjadi beberapa kelas.

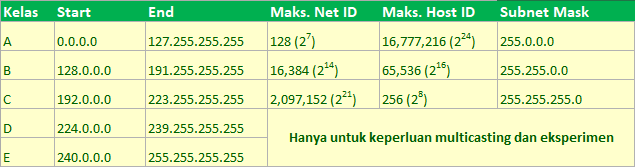
Kelass IP Address

Pada dasarnya IP Address terdiri atas 4 oktet, misal 192.168.1.2, dimana 192 adalah oktet pertama, 168 okter kedua dan seterusnya. Nilai dari 1 oktet adalah maksimal 255. Untuk menggolongkan IP Address sebanyak itu maka dibentuk 5 kelas dan terdiri dari kelas A sampai kelas E (kelas D dan E sangat jarang digunakan). Masing – masing kelas memegang peranan penting dalam sistem jaringan komputer. Selain itu dikenal pula istilah Network ID (Net ID) dan Host ID yang memang identik dengan penggunaan IP Address (kecuali IP Address kelas D dan E).

1. Untuk IP Address kelas A biasa digunakan pada sistem jaringan skala besar. Bit pertama diawali dengan angka 0. Untuk panjang Network ID adalah 1 oktet sedangkan panjang Host ID 3 oktet. Jumlah host pada kelas A dapat mencapai 16.777.216.
2. Untuk IP Address kelas B biasanya lebih sering digunakan pada sistem jaringan skala besar dan menengah dengan daya tampung mencapai kurang lebih 65.536 host diseluruh dunia. Panjang Network ID pada kelas ini adalah 2 oktet sedangkan panjang Host ID 2 oktet.
3. Untuk IP Address kelas C biasa digunakan pada sistem jaringan skala kecil dengan daya tampung hanya 256 host. Untuk panjang Network ID adalah 3 oktet sedangkan panjang Host ID 1 oktet.
4. Untuk IP Address kelas D digunakan khusus untuk keperluan multicasting, dimana IP address (host) awal adalah 224.0.0.0 hingga 239.255.255.255. Dalam multicasting juga tidak mengenal istilah Network ID dan Host ID.
5. Untuk IP Address kelas E dicadangkan hanya untuk keperluan eksperimental saja, dimana IP address (host) awal adalah 240.0.0.0 hingga 255.255.255.255. Sama halnya dengan Kelas D, IP Address kelas E juga tidak mengenal istilah Network ID dan Host ID.

Itulah artikel mengenai pengertian IP address beserta fungsi dan kelas IP address yang perlu anda ketahui. Dengan artikel diatas, semoga anda menjadi lebih paham mengenai apa itu IP address, kegunaannya untuk apa dan ada berapa kelas pada IP address.

https://www.nesabamedia.com/pengertian-ip-address-dan-fungsi-ip-address/

Bilangan biner

Penjelasan Bilangan Biner Lengkap dengan Contoh Soalnya

Pengertian Bilangan Biner – Definisi Bilangan Biner atau dalam Bahasa Inggris “Binary” adalah sebuah jenis penulisan angka menggunakan dua simbol yaitu 0 dan 1. Sistem bilangan biner adalah sebuah dasar dari semua bilangan berbasis digital. Dari bilangan biner kita bisa mengkonversi ke bilangan desimal. Sistem bilangan biner bisa juga disebut dengan bit atau Binary digit. Pengelompokan biner dalam istilah komputer selalu berjumlah 8, dengan istilah 1 Byte. Jangan sampai salah antara byte dan bit itu berbeda, 1 byte sama dengan 8 bit. Sistem coding komputer secara umum menggunakan sistem coding 1 byte. Bilangan biner yang digunakan itu ada 8 digit angka yang hanya berisikan angka 1 dan 0, tidak ada angka yang lain.

Sistem bilangan Biner pertama kali digunakan di awal abad 70-an oleh Thomas Harriot. Dalam bilangan biner sama seperti bilangan lainnya, berlaku juga penambahan biner, pengurangan biner, perkalian biner dan pembagian biner.

Artikel Terkait:

• Penjelasan Nilai Mutlak dan contohnya
• Macam-macam rumus Geometri

Daftar Isi [hide]

• 1 Skema Bilangan Biner
  • 1.1 Bilangan Biner dan Desimal
    • 1.1.1 Cara Penjumlahan Bilangan Biner
    • 1.1.2 Cara Pengurangan Bilangan Biner
  • 1.2 Konversi Bilangan Biner ke Desimal
    • 1.2.1 Contoh Soal Konversi Bilangan Biner ke Desimal
    • 1.2.2 Topik yang berhubungan

Skema Bilangan Biner

Desimal	Biner (8 bit )
0	0000 0000
1	0000 0001
2	0000 0010
3	0000 0011
4	0000 0100
5	0000 0101
6	0000 0110
7	0000 0111
8	0000 1000
9	0000 1001
10	0000 1010
11	0000 1011
12	0000 1100
13	0000 1101
14	0000 1110
15	0000 1111
16	0001 0000

Bilangan Biner dan Desimal

Angka desimal setara dengan bilangan biner, di bawah ini Anda bisa melihat grafik angka biner. 0 dan 1 yang umum untuk kedua biner dan desimal. Nilai desimal 2 di biner diberikan di bawah ini. Angka-angka biner disebut sebagai bit dalam studi komputer.

Cara Penjumlahan Bilangan Biner

Kita ambil sebagai sampel soal yaitu :

1101(2)+1011(2)=……(2)?

1011(2)+0111(2)=…….(2)?

Jawab :

1101(2)

1011(2)

_____+

11000(2)

1+1=0 mempunyai carry(sisa) 1

1+0+1=0 carry 1

1+1+0=0 carry 1

1+1+1=1 carry 1

jadi hasil total adalah : 1111(2)

Cara Pengurangan Bilangan Biner

Mari kita jawab contoh soal pengurangan sistem bilangan biner berikut :

1110(2)-0101(2)=….(2)?

1011(2)-111(2)=….(2)?

Jawab :

1110(2)

0101(2)

_______+

10001(2)

0-1=1 borrow/pinjam sebelah 1

0-0=0 1 jadi nol karena dipinjam 1

1-1=0

1-0=1

Jadi total adalah :  10001(2)

Konversi Bilangan Biner ke Desimal

Ada perbedaan dalam sistem Bilangan Biner dan desimal, dalam komputer data yang disimpan menggunakan bilangan biner, hanya menggunakan nol dan satu untuk mewakili semua data, jadi jika ingin melihat data yang lebih mudah dipahami, maka kita harus mengkonversinya ke bilangan desimal. Berikut ini cara Konversi bilangan Biner ke desimal Menggunakan Notasi Posisi, dikutip dari wikihow.com.

1. Tuliskan angka biner dan daftar kuadrat 2 dari kanan ke kiri. Misalnya kita ingin mengubah angka biner 100110112 menjadi desimal. Pertama, tuliskan. Kemudian, tuliskan kuadrat 2 dari kanan ke kiri. Mulailah dari 20, yaitu 1. Kenaikan kuadrat satu per satu. Hentikan jika jumlah angka yang ada di daftar sama dengan banyaknya digit angka biner. Contoh angkanya, 10011011, memiliki delapan digit, jadi daftarnya memiliki 8 angka, seperti ini: 128, 64, 32, 16, 8, 4, 2, 1
2. 2. Tuliskan digit angka biner di bawah daftar kuadrat dua. Tuliskan angka 10011011 di bawah angka 128, 64, 32, 16, 8, 4, 2, dan 1 sehingga setiap digit biner memiliki kuadrat angka duanya masing-masing. Angka 1 di kanan angka biner sejajar dengan angka 1 dalam daftar kuadrat 2 dan selanjutnya. Anda juga bisa menuliskan digit biner di atas daftar kuadrat dua, jika Anda lebih memilihnya. Yang penting adalah Anda bisa memasangkannya.
3. Hubungkan digit dari angka biner dengan daftar kuadrat dua. Buatlah garis, mulai dari kanan, menghubungkan setiap digit angka biner dengan kuadrat dua. Mulailah memberi garis dari digit pertama angka biner dengan kuadrat angka dua pertama dalam daftar yang ada di atasnya. Kemudian, tariklah garis dari digit kedua angka biner ke kuadrat angka dua kedua dalam daftar. Lanjutkan menghubungkan setiap digit dengan kuadrat dua. Hal ini akan membantu Anda dalam membayangkan hubungan antara kedua kumpulan angka.
4. Tuliskan nilai akhir setiap kuadrat dua. Sisirlah setiap digit angka biner. Jika digitnya adalah 1, tulislah kuadrat dua pasangannya di bawah angka 1 tersebut. Jika digitnya adalah 0, tulislah 0 di bawah angka 0.

Karena 1 berpasangan dengan 1, hasilnya adalah 1. Karena 2 berpasangan dengan 1, hasilnya adalah 2. Karena 4 berpasangan dengan 0, hasilnya adalah 0. Karena 8 berpasangan dengan 1, hasilnya adalah 8, dan karena 16 berpasangan dengan 1, hasilnya adalah 16. 32 berpasangan dengan 0 sehingga hasilnya 0 dan 64 berpasangan dengan 0 sehingga hasilnya adalah 0, sedangkan 128 berpasangan dengan 1 sehingga hasilnya 128.

5. Tambahkan nilai akhirnya. Sekarang, tambahkan semua angka yang tertulis di bawah digit angka biner. Inilah yang Anda lakukan: 128 + 0 + 0 + 16 + 8 + 0 + 2 + 1 = 155. Ini adalah angka desimal yang setara dengan angka biner 10011011.
6. Tulislah jawaban Anda dengan subskrip basisnya. Sekarang, Anda harus menulis 15510, untuk menunjukkan bahwa angka itu adalah desimal, yang memiliki kelipatan 10. Semakin Anda terbiasa mengubah biner menjadi desimal, akan lebih mudah untuk Anda mengingat kuadrat dua, dan Anda akan mampu mengubahnya dengan lebih cepat.
7. Gunakan cara ini untuk mengubah angka biner dengan titik desimal ke dalam bentuk desimal. Anda bisa menggunakan cara ini saat Anda ingin mengubah angka biner seperti 1,12 menjadi desimal. Yang harus Anda lakukan adalah mengetahui bahwa angka di bagian kiri desimal adalah posisi satuan, sedangkan angka di bagian kanan desimal adalah posisi setengah, atau 1 x (1/2).

Angka 1 di bagian kiri titik desimal sama dengan 20, atau 1. Angka 1 di bagian kanan desimal sama dengan 2-1, atau 0,5. Tambahkan 1 dan 0,5 sehingga hasilnya 1,5 yang dapat ditulis 1,12 dalam notasi desimal.

Contoh Soal Konversi Bilangan Biner ke Desimal

Pertanyaan 1: Coba konversi 1101 ke angka desimal?

Jawab:

bilangan biner adalah 1101.

Jadi, 1101 = (1 X 2 3 ) + (1 X 2 2 ) + (0 X 2 1 ) + (1 X 2 0 )

= (1 X 8) + (1 X 4) + (0 X 2) + (1 X 1)

= 8 + 4 + 0 + 1

Jawaban yang benar adalah 13

Pertanyaan 2: Coba konversi 1001 ke angka desimal?

Jawab:

bilangan biner adalah 1001.

Jadi, 1001 = (1 X 2 3 ) + (0 X 2 2 ) + (0 X 2 1 ) + (1 X 2 0 )

= (1 X 8) + (0 X 4) + (0 X 2) + (1 X 1)

= 8 + 0 + 0 + 1

Jawaban yang benar adalah 9

Pertanyaan 3: Coba konversi 01.011.101 ke angka desimal?

Jawab:

bilangan biner adalah 01011101.

01011101 = (0 X 2 7 ) + (1 X 2 6 ) + (0 X 2 5 ) + (1 X 2 4 ) + (1 X 2 3 ) + (1 X 2 2 ) + (0 X 2 1 ) + (1 X 2 0 )

= (0 X 128) + (1 X 64) + (0 X 32) + (1 X 16) + (1 X 8) + (1 X 4) + (0 X 2) + (1 X 1)

= + 64 + 0 0 + 16 + 8 + 4 + 0 + 1

Jawaban yang benar adalah 93

Pertanyaan 4: Convert 01.100,011 ke desimal jumlah? Jawaban yang benar adalah 12,375

Oke, demikian penjelasan Broexcel untuk pengertian Bilangan Biner, cara penghitungan dan contoh soal latihannya, jangan lupa update terus informasi ilmu pengetahuan anda seputar rumus matematika dan rumus Microsoft Excel hanya di Broexcel.com.

Topik yang berhubungan

• contoh soal bilangan biner beserta jawabannya
• bilangan biner
• contoh soal bilangan biner
• angka biner
• biner
• contoh bilangan biner
• contoh soal biner
• contoh soal bilangan biner dan penyelesaiannya
• bilangan biner adalah
• sistem bilangan biner https://www.broexcel.com/penjelasan-bilangan-biner-dan-contoh-soalnya.html

Bilangan biner

Penjelasan Bilangan Biner Lengkap dengan Contoh Soalnya

Pengertian Bilangan Biner – Definisi Bilangan Biner atau dalam Bahasa Inggris “Binary” adalah sebuah jenis penulisan angka menggunakan dua simbol yaitu 0 dan 1. Sistem bilangan biner adalah sebuah dasar dari semua bilangan berbasis digital. Dari bilangan biner kita bisa mengkonversi ke bilangan desimal. Sistem bilangan biner bisa juga disebut dengan bit atau Binary digit. Pengelompokan biner dalam istilah komputer selalu berjumlah 8, dengan istilah 1 Byte. Jangan sampai salah antara byte dan bit itu berbeda, 1 byte sama dengan 8 bit. Sistem coding komputer secara umum menggunakan sistem coding 1 byte. Bilangan biner yang digunakan itu ada 8 digit angka yang hanya berisikan angka 1 dan 0, tidak ada angka yang lain.

Sistem bilangan Biner pertama kali digunakan di awal abad 70-an oleh Thomas Harriot. Dalam bilangan biner sama seperti bilangan lainnya, berlaku juga penambahan biner, pengurangan biner, perkalian biner dan pembagian biner.

Artikel Terkait:

• Penjelasan Nilai Mutlak dan contohnya
• Macam-macam rumus Geometri

Daftar Isi [hide]

• 1 Skema Bilangan Biner
  • 1.1 Bilangan Biner dan Desimal
    • 1.1.1 Cara Penjumlahan Bilangan Biner
    • 1.1.2 Cara Pengurangan Bilangan Biner
  • 1.2 Konversi Bilangan Biner ke Desimal
    • 1.2.1 Contoh Soal Konversi Bilangan Biner ke Desimal
    • 1.2.2 Topik yang berhubungan

Skema Bilangan Biner

Desimal	Biner (8 bit )
0	0000 0000
1	0000 0001
2	0000 0010
3	0000 0011
4	0000 0100
5	0000 0101
6	0000 0110
7	0000 0111
8	0000 1000
9	0000 1001
10	0000 1010
11	0000 1011
12	0000 1100
13	0000 1101
14	0000 1110
15	0000 1111
16	0001 0000

Bilangan Biner dan Desimal

Angka desimal setara dengan bilangan biner, di bawah ini Anda bisa melihat grafik angka biner. 0 dan 1 yang umum untuk kedua biner dan desimal. Nilai desimal 2 di biner diberikan di bawah ini. Angka-angka biner disebut sebagai bit dalam studi komputer.

Cara Penjumlahan Bilangan Biner

Kita ambil sebagai sampel soal yaitu :

1101(2)+1011(2)=……(2)?

1011(2)+0111(2)=…….(2)?

Jawab :

1101(2)

1011(2)

_____+

11000(2)

1+1=0 mempunyai carry(sisa) 1

1+0+1=0 carry 1

1+1+0=0 carry 1

1+1+1=1 carry 1

jadi hasil total adalah : 1111(2)

Cara Pengurangan Bilangan Biner

Mari kita jawab contoh soal pengurangan sistem bilangan biner berikut :

1110(2)-0101(2)=….(2)?

1011(2)-111(2)=….(2)?

Jawab :

1110(2)

0101(2)

_______+

10001(2)

0-1=1 borrow/pinjam sebelah 1

0-0=0 1 jadi nol karena dipinjam 1

1-1=0

1-0=1

Jadi total adalah :  10001(2)

Konversi Bilangan Biner ke Desimal

Ada perbedaan dalam sistem Bilangan Biner dan desimal, dalam komputer data yang disimpan menggunakan bilangan biner, hanya menggunakan nol dan satu untuk mewakili semua data, jadi jika ingin melihat data yang lebih mudah dipahami, maka kita harus mengkonversinya ke bilangan desimal. Berikut ini cara Konversi bilangan Biner ke desimal Menggunakan Notasi Posisi, dikutip dari wikihow.com.

1. Tuliskan angka biner dan daftar kuadrat 2 dari kanan ke kiri. Misalnya kita ingin mengubah angka biner 100110112 menjadi desimal. Pertama, tuliskan. Kemudian, tuliskan kuadrat 2 dari kanan ke kiri. Mulailah dari 20, yaitu 1. Kenaikan kuadrat satu per satu. Hentikan jika jumlah angka yang ada di daftar sama dengan banyaknya digit angka biner. Contoh angkanya, 10011011, memiliki delapan digit, jadi daftarnya memiliki 8 angka, seperti ini: 128, 64, 32, 16, 8, 4, 2, 1
2. 2. Tuliskan digit angka biner di bawah daftar kuadrat dua. Tuliskan angka 10011011 di bawah angka 128, 64, 32, 16, 8, 4, 2, dan 1 sehingga setiap digit biner memiliki kuadrat angka duanya masing-masing. Angka 1 di kanan angka biner sejajar dengan angka 1 dalam daftar kuadrat 2 dan selanjutnya. Anda juga bisa menuliskan digit biner di atas daftar kuadrat dua, jika Anda lebih memilihnya. Yang penting adalah Anda bisa memasangkannya.
3. Hubungkan digit dari angka biner dengan daftar kuadrat dua. Buatlah garis, mulai dari kanan, menghubungkan setiap digit angka biner dengan kuadrat dua. Mulailah memberi garis dari digit pertama angka biner dengan kuadrat angka dua pertama dalam daftar yang ada di atasnya. Kemudian, tariklah garis dari digit kedua angka biner ke kuadrat angka dua kedua dalam daftar. Lanjutkan menghubungkan setiap digit dengan kuadrat dua. Hal ini akan membantu Anda dalam membayangkan hubungan antara kedua kumpulan angka.
4. Tuliskan nilai akhir setiap kuadrat dua. Sisirlah setiap digit angka biner. Jika digitnya adalah 1, tulislah kuadrat dua pasangannya di bawah angka 1 tersebut. Jika digitnya adalah 0, tulislah 0 di bawah angka 0.

Karena 1 berpasangan dengan 1, hasilnya adalah 1. Karena 2 berpasangan dengan 1, hasilnya adalah 2. Karena 4 berpasangan dengan 0, hasilnya adalah 0. Karena 8 berpasangan dengan 1, hasilnya adalah 8, dan karena 16 berpasangan dengan 1, hasilnya adalah 16. 32 berpasangan dengan 0 sehingga hasilnya 0 dan 64 berpasangan dengan 0 sehingga hasilnya adalah 0, sedangkan 128 berpasangan dengan 1 sehingga hasilnya 128.

5. Tambahkan nilai akhirnya. Sekarang, tambahkan semua angka yang tertulis di bawah digit angka biner. Inilah yang Anda lakukan: 128 + 0 + 0 + 16 + 8 + 0 + 2 + 1 = 155. Ini adalah angka desimal yang setara dengan angka biner 10011011.
6. Tulislah jawaban Anda dengan subskrip basisnya. Sekarang, Anda harus menulis 15510, untuk menunjukkan bahwa angka itu adalah desimal, yang memiliki kelipatan 10. Semakin Anda terbiasa mengubah biner menjadi desimal, akan lebih mudah untuk Anda mengingat kuadrat dua, dan Anda akan mampu mengubahnya dengan lebih cepat.
7. Gunakan cara ini untuk mengubah angka biner dengan titik desimal ke dalam bentuk desimal. Anda bisa menggunakan cara ini saat Anda ingin mengubah angka biner seperti 1,12 menjadi desimal. Yang harus Anda lakukan adalah mengetahui bahwa angka di bagian kiri desimal adalah posisi satuan, sedangkan angka di bagian kanan desimal adalah posisi setengah, atau 1 x (1/2).

Angka 1 di bagian kiri titik desimal sama dengan 20, atau 1. Angka 1 di bagian kanan desimal sama dengan 2-1, atau 0,5. Tambahkan 1 dan 0,5 sehingga hasilnya 1,5 yang dapat ditulis 1,12 dalam notasi desimal.

Contoh Soal Konversi Bilangan Biner ke Desimal

Pertanyaan 1: Coba konversi 1101 ke angka desimal?

Jawab:

bilangan biner adalah 1101.

Jadi, 1101 = (1 X 2 3 ) + (1 X 2 2 ) + (0 X 2 1 ) + (1 X 2 0 )

= (1 X 8) + (1 X 4) + (0 X 2) + (1 X 1)

= 8 + 4 + 0 + 1

Jawaban yang benar adalah 13

Pertanyaan 2: Coba konversi 1001 ke angka desimal?

Jawab:

bilangan biner adalah 1001.

Jadi, 1001 = (1 X 2 3 ) + (0 X 2 2 ) + (0 X 2 1 ) + (1 X 2 0 )

= (1 X 8) + (0 X 4) + (0 X 2) + (1 X 1)

= 8 + 0 + 0 + 1

Jawaban yang benar adalah 9

Pertanyaan 3: Coba konversi 01.011.101 ke angka desimal?

Jawab:

bilangan biner adalah 01011101.

01011101 = (0 X 2 7 ) + (1 X 2 6 ) + (0 X 2 5 ) + (1 X 2 4 ) + (1 X 2 3 ) + (1 X 2 2 ) + (0 X 2 1 ) + (1 X 2 0 )

= (0 X 128) + (1 X 64) + (0 X 32) + (1 X 16) + (1 X 8) + (1 X 4) + (0 X 2) + (1 X 1)

= + 64 + 0 0 + 16 + 8 + 4 + 0 + 1

Jawaban yang benar adalah 93

Pertanyaan 4: Convert 01.100,011 ke desimal jumlah? Jawaban yang benar adalah 12,375

Oke, demikian penjelasan Broexcel untuk pengertian Bilangan Biner, cara penghitungan dan contoh soal latihannya, jangan lupa update terus informasi ilmu pengetahuan anda seputar rumus matematika dan rumus Microsoft Excel hanya di Broexcel.com.

Topik yang berhubungan

• contoh soal bilangan biner beserta jawabannya
• bilangan biner
• contoh soal bilangan biner
• angka biner
• biner
• contoh bilangan biner
• contoh soal biner
• contoh soal bilangan biner dan penyelesaiannya
• bilangan biner adalah
• sistem bilangan biner

https://www.broexcel.com/penjelasan-bilangan-biner-dan-contoh-soalnya.html